|
|
|
FUNCTIA DE TRANSFER A UNEI MASINI DE CURENT CONTINUU
1. Masina de curent continuu cu excitatie separata
Este necesara cunoasterea functiei de transfer a unei masini de curent continuu pentru a putea analiza stabilitatea statica a functionarii acesteia si pentru a putea realiza proiectarea actionarii in bucla inchisa. Sistemele in bucla inchisa sunt utilizate atunci cand se doreste obtinerea unor rezultate foarte bune in controlul vitezei sau al pozitiei.
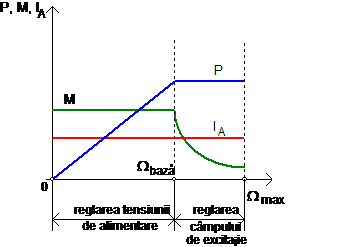
Fig. 2.21. Variatia cuplului, a puterii si a curentului in cazul reglajului combinat, la sarcina constanta.
Circuitul echivalent al masinii de curent continuu cu excitatie independenta este prezentat in figura 2.22.
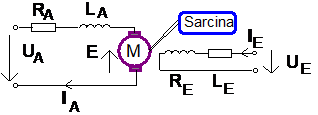
Fig. 2.22. Circuitul echivalent al
masinii de curent continuu cu excitatie independenta.
Functia de transfer a masinii va fi prezentata atat in cazul reglarii tensiunii de alimentare, cat si in cazul reglarii campului de excitatie.
1.1. Reglarea tensiunii de alimentare
In relatiile ce vor urma vom nota cu litere mici marimile ce variaza in functie de timp.
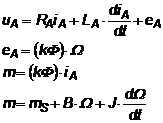(2.70
- 2.73)
unde B, reprezinta coeficientul de frecari vascoase.
Daca sistemului de ecuatii anterior, ii aplicam transformata Laplace considerand conditii initiale nule, obtinem urmatoarele relatii:
(2.74 -
2.75)
unde X(s) reprezinta transformata Laplace a marimii x(t). Daca notam constanta mecanica datorata frecarilor vascoase cu:
(2.76)
cu ajutorul relatiilor 2.35 - 2.36, din 2.74, pentru curent obtinem:
(2.77)
iar din 2.75, pentru viteza obtinem:
(2.78)
Pe baza ultimelor relatii, poate fi construita schema bloc a masinii:
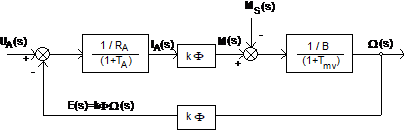
Fig. 2.23. Schema bloc a masinii de curent continuu cu excitatie independenta comandata pe indus.
Conform schemei prezentate, se observa ca masina se comporta ca un sistem in bucla inchisa cu marimea de reactie egala cu tensiunea electromotoare E si cu doua intrari: tensiunea de alimentare si cuplul de sarcina. Rezulta ca in studiul comportarii masinii de curent continuu sunt utile in general doua functii de transfer (iesirea sistemului raportata la o intrare), viteza unghiulara a masinii in functie de tensiunea de alimentare si viteza in functie de cuplul de sarcina. Sistemele de actionare electrica cu masini de curent continuu alimentate de la convertoare cu semiconductoare necesita exprimarea vitezei functie de tensiunea de alimentare. Pentru obtinerea acestei functii de transfer, vom pasiviza cea de-a doua intrare, cuplul de sarcina, exprimand pe rand viteza functie de curentul prin indusul masinii si curentul functie de tensiunea de alimentare. Daca consideram cuplul de sarcina nul in relatia 2.78, obtinem:
(2.79)
si inlocuind in 2.77, rezulta:
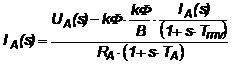(2.80)
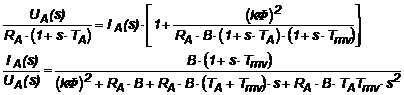
(2.81 - 2.82)
Cu folosirea notatiilor:
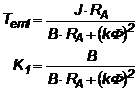(2.83
- 2.84)
rezulta:
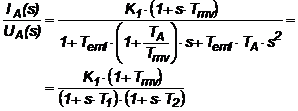(2.85)
cu T1 si T2 radacinile numitorului. Aceste
valori sunt complex conjugate pentru o gama destul de larga de masini de
curent continuu cu excitatie independenta, ce au conectate in serie cu
indusul o inductivitate de filtrare. Pentru masinile care au constanta
electrica mult mai mica decat cea electromecanica, numitorul relatiei 2.85
devine: (
).
Functia de transfer globala rezulta din combinarea relatiilor 2.79 si 2.85:
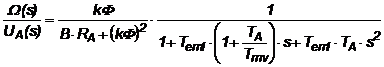
(2.86)
Astfel, indata ce a fost stabilita functia de transfer si respectiv schema bloc echivalenta a masinii de curent continuu, se poate realiza schema structurala a intregului sistem de actionare electrica in vederea proiectarii partii de comanda si reglare. Schema este utila pentru studierea comportarii ansamblului la diferite semnale standard de intrare (semnal de tip treapta, rampa, sinusoidal, etc.), precum si influenta asupra iesirii a diferitilor parametri ai sistemului, aspecte prezentate in capitolul 5.
1.2. Reglarea campului de excitatie
In cadrul unor sisteme de actionari electrice, viteza este reglata cu ajutorul metodei ce presupune slabirea de camp, dar prin considerarea unui curent constant prin indusul masinii (mentinerea unei valori constante este facuta printr-un sistem in bucla inchisa). Modificarea curentului prin indus datorita variatiei curentului de excitatie se poate neglija, daca se are in vedere valoarea foarte mica a constantei de timp rotorice prin comparatie cu cea a excitatiei. Din circuitul echivalent prezentat in figura 2.22, rezulta:
(2.87)
si considerand un
circuit magnetic linear, pentru 
, rezulta:
(2.88)
Cu relatiile anterioare si cu 2.73, avem:
(2.89)
In continuare aplicam transformata Laplace si determinam relatia pentru viteza unghiulara:
(2.90 - 2.91)
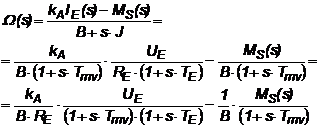(2.92)
unde: 
(2.93)
reprezinta constanta electrica a circuitului de excitatie.
Daca cuplul de sarcina depinde de viteza, atunci el este adaugat cuplului de frecari vascoase, rezultand o alta valoare pentru constanta B. Relatia 2.92 se poate reprezenta astfel:
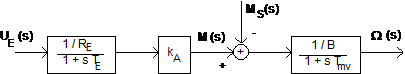
Fig. 2.24. Schema bloc a masinii de curent continuu cu excitatie independenta comandata prin circuitul de excitatie.
2. Masina de curent continuu cu excitatie serie
Trebuie mentionat de la inceput, ca in cazul unui sistem de actionare cu o comanda in bucla inchisa, reglarea curentului prin indus reprezinta totodata si reglarea curentului de excitatie al masinii. Schema bloc a masinii de curent continuu cu excitatie serie se determina similar cu cazul prezentat anterior. Ipotezele si consideratiile facute in cadrul acestui capitol raman valabile si aici. Circuitul echivalent de la care se pleaca are la baza schema din figura 2.4.a. Acum, constanta electrica a masinii este data de relatia:
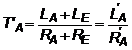(2.94)
unde 
este rezistenta
tuturor elementelor inseriate cu indusul masinii de curent continuu cu
excitatie serie: infasurarea de excitatie; infasurarea de
compensatie; infasurarea de comutatie;
este inductivitatea
proprie a indusului impreuna cu cea a infasurarii de excitatie.
Astfel modelul matematic al masinii de curent
continuu cu excitatie serie se obtine din sistemul de ecuatii
2.70-2.73 in care se inlocuieste 
cu , 
cu si este adaugata
relatia de dependenta a fluxului de excitatie de curentul de
sarcina:
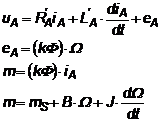(2.95
- 2.98)
(2.99)
Pentru rezolvarea sistemului de ecuatii 2.95-2.99 trebuie utilizata o metoda de linearizare a acestuia. Cea mai des folosita metoda este aceea de linearizare a modelului matematic in jurul unui punct de functionare. Modelul matematic se scrie pentru variatii mici ale marimilor functionale.
Ecuatia 2.99 si respectiv dependenta
vitezei unghiulare a masinii de valoarea curentului de sarcina, pentru
aceste variatii mici (abateri mici)
este scrisa in functie de tangenta la functia respectiva in punctul
de functionare considerat (
pentru tangenta la caracteristica fluxului de excitatie
si respectiv 
tangenta la
caracteristica mecanica a masinii).
Din acest punct tratarea problemei functiei de transfer a masinii de curent continuu cu excitatie serie si respectiv reprezentarea acesteia sub forma unei scheme bloc decurge ca in cazul masinii de curent continuu cu excitatie separata. In urma aplicarii transformatei Laplace se obtine o schema bloc echivalenta identica cu cea prezentata in figura 2.23
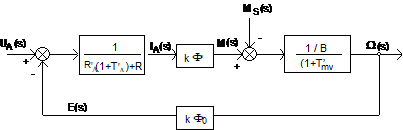
Fig. 2.25. Schema bloc a
masinii de curent continuu cu excitatie serie.
unde: 
;
.
Din aceste relatii se observa ca masina de curent continuu cu excitatie serie introduce un termen proportional cu viteza unghiulara, deci practic o componenta de tipul frecare vascoasa, ce are o importanta semnificativa in stabilitatea intregului sistem de actionare electrica.
PROBLEME
1. Probleme rezolvate
PR1. Un motor de curent continuu cu excitatie separata are turatia nominala egala cu 500rot/min si actioneaza o sarcina ce are cuplul proportional cu viteza. Tensiunea nominala a masinii este de 220V, curentul nominal de 20A.
Ce rezistenta trebuie conectata in serie cu indusul masinii pentru a reduce viteza actionarii la 250rot/min, daca rezistenta indusului este de 1?
Rezolvare 
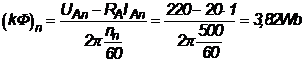
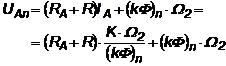
si rezulta:
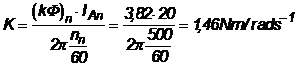
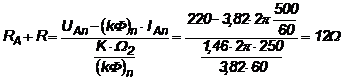
PR2. Un motor de curent continuu cu excitatie separata are urmatoarele date nominale:
Motorul antreneaza sub valorile limita o sarcina ce are cuplu constant si independent de viteza. Modificarea vitezei la valori inferioare vitezei de mers in gol se face prin intermediul reglarii tensiunii la bornele masinii, iar pentru valori superioare vitezei de mers in gol, prin reglarea valorii fluxului de excitatie (slabire de camp). Se cere:
a) Care este tensiunea la bornele indusului masinii, daca viteza unghiulara are valoarea de 400rot/min?
b) De cate ori trebuie redus fluxul de excitatie pentru a obtine o viteza unghiulara de 800rot/min?
Rezolvare
a) 
b)
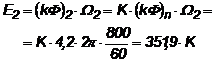
Cuplul de sarcina fiind constant, avem:
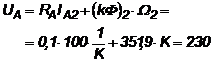
si
rezulta 
si 
. Conform acestor valori, solutia acceptata este prima
si astfel pentru cresterea vitezei unghiulare a actionarii la
valoarea de 800 rot/min, fluxul de excitatie va trebui scazut de 0,61 ori,
adica cu circa 40% fata de valoarea sa nominala.
2. Probleme propuse
PP1. O actionare electrica cu grup generator-motor este realizata cu doua masini de curent continuu cu excitatie separata identice si un motor asincron trifazat. Datele nominale ale masinilor sunt urmatoarele:
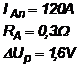
si raportul pierderilor mecanice si de ventilatie la pierderile Joule nominale din indusul unei masini de curent continuu de 1/1,5.
Se considera neglijabile pierderile suplimentare si efectul demagnetizant al reactiei indusului. Se cere:
a) Ce putere trebuie sa aiba motorul asincron de antrenare, daca motorul de curent continuu trebuie sa functioneze in regim nominal? Se considera pierderile de putere ale celor doua masini de curent continuu, egale.
b) Care va fi turatia de mers in gol a motorului de curent continuu, daca turatia motorului asincron scade cu puterea dezvoltata relativa conform relatiei:
?
c). Care va fi turatia nominala a motorului de curent continuu, daca turatia motorului asincron scade cu puterea dezvoltata relativa conform relatiei anterioare?
Se va considera ca pierderile mecanice si de ventilatie ale masinilor de curent continuu au valoarea nominala, iar generatorul are excitatie nominala. Puterea la mersul in gol a motorului asincron, se estimeaza in conditiile date la 10% din puterea nominala a cestuia.
PP2. Un motor de curent continuu cu excitatie derivatie are urmatoarele date nominale:
Se considera curentul de excitatie constant si egal cu valoarea sa nominala. Pentru pornirea masinii se utilizeaza o schema de comanda secventiala in functie de timp cu ajutorul unui reostat de pornire cu trei trepte. Schema permite obtinerea acelorasi valori ale curentului minim, respectiv maxim de pornire pe durata procesului tranzitoriu. Valoarea minima este cu 10% mai mare decat valoarea curentului nominal al masinii. Se cere:
a). Care este valoarea minima si respectiv maxima a curentului de pornire? Se considera reactia indusului, caderea de tensiune la perii si inductivitatea indusului neglijabile.
b). Sa se determine valorile treptelor reostatului de pornire.
c). Daca cuplul
de sarcina este proportional cu viteza 
Nm, sa se determine
variatia turatiei la pornire.
d). Sa se determine timpul de functionare pe fiecare treapta a reostatului de pornire, precum si timpul total de pornire.
Momentul total de inertie raportat la arborele masinii este 7 kgm2.
PP3. Pentru masina de curent continuu cu excitatie derivatie din problema precedenta sa se determine schema bloc echivalenta atat in prezenta cuplului de sarcina, cat si in absenta sa.
2.7. BIBLIOGRAFIE
1. Bose B.K. "Power Electronics and AC Drives", Prentice-Hall, Inc., 1986;
2. Dubey G.K. "Power Semiconductor Controlled Drives", Prentice-Hall, Inc., 1989;
3. Fransua Al., Magureanu R. "Masini si actionari electrice", Ed. Tehnica, 1986;
4. Fransua Al., Magureanu R., Tocaci M. "Masini si actionari electrice. Culegere de probleme", E.D.P.B., 1980;
5. Hoft R.G. "Semiconductor Power Supplies", New York, Van Nostrand, 1986;
6. Kelemen A. "Actionari electrice", E.D.P.B., 1979;
7. Kyyrä J. "Suuntaajatekniikka", Helsinki, Otaniemi, 1995;
8. Leonhard W. "Control of Electrical Drives", Spriger Ferlag, 1985;
9. Mard M. "Sähkökäyttö", Helsinki, Otaniemi, 1995
10.Navrapescu V. "Referatul 2 de doctorat", Sept. 1994;
11.Micu E. "Electrotehnica de la A la Z", Ed. Stiintifica si Enciclopedica, 1985;
12.Soran I.F. "Actionari Electrice", Lito IPB, 1988;
13.Tunsoiu Gh., Seracin E., Saal C. "Actionari Electrice", EDPB, 1982.
