
|
|
|
Notatia in complement fata de doi. Adunarea numerelor reprezentate in complement fata de doi.
Problema depasirii superioare (1.5: 1.5.2, 1.5.3, 1.5.4)
Cel mai popular sistem de reprezentare a numerelor intregi in cadrul calculatoarelor actuale este notatia in complement fata de doi (two's complement notation). Acest sistem utilizeaza un numar fix de biti pentru a reprezenta valorile din cadrul sistemului. Figura 1.22 prezinta sistemele in complement fata de doi bazate pe cuvinte de cod de lungime 3 si 4. Pentru constructia unui astfel de sistem, se incepe cu un sir de biti de valoarea 0 de lungime adecvata si apoi se numara in binar pana cand se ajunge la un sir de biti care incepe cu un bit 0,1,2,3, .
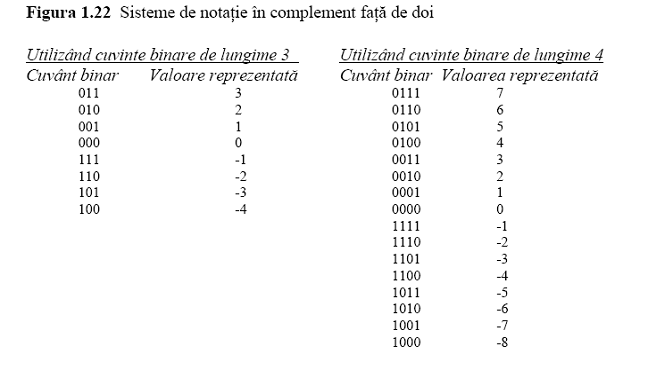
Cuvintele care reprezinta valorile negative se obtin incepand cu un sir de biti cu valoarea 1 si numarand in sens descrescator pana la atingerea cuvantului care incepe cu un bit 1 si are toti ceilalti biti zero. Cuvintele astfel obtinute reprezinta valorile -1, -2, -3, Observati ca in sistemul de notatie in complement fata de doi valorile negative sunt reprezentate de cuvinte al caror bit de semn este 1; in schimb, un bit de semn egal cu 0 indica faptul ca valoarea reprezentata este zero sau pozitiva.. Aceste reprezentari sunt identice atunci cand sunt citite de la dreapta la stanga, pana la inclusiv primul bit de 1 din cuvant. De aici fiecare cuvant este complementul celuilalt. (Complementul unui cuvant binar este cuvantul obtinut prin schimbarea tuturor bitilor de 1 la valoarea 0, respectiv a tuturor bitilor 0 in 1; cuvantul 0110 este complementul lui 1001 si invers.) De exemplu, in sistemul de codificare pe patru biti din figura 1.21 cuvintele care reprezinta valorile 2 si -2 se termina amandoua cu 10, dar cuvantul corespunzator valorii 2 incepe cu 00, in timp ce reprezentarea valorii -2 incepe cu 11.
Aceasta observatie conduce la realizarea unui algoritm care sa permita obtinerea reprezentarii binare pentru valori de semne contrare dar care au acelasi modul. Vom copia cuvantul original incepand de la dreapta pana la aparitia unui bit cu valoarea 1, apoi vom face complementul bitilor ramasi (vom schimba toti biti 1 ramasi in 0 si toti bitii 0 in 1) pe masura ce-i copiem
Intelegerea acestor proprietatii elementare ale sistemelor in complement fata de doi conduce de asemenea la obtinerea unui algoritm pentru decodificarea reprezentarilor in complement fata de doi. Daca modelul de biti ce trebuie decodificat are bitul de semn zero, se va citi direct valoarea ca si cum cuvantul ar fi o reprezentare binara normala. De exemplu, 0110 reprezinta valoarea 6, deoarece 110 este reprezentarea binara a lui 6. Daca sablonul care trebuie decodificat are bitul de semn 1, vom intelege ca valoarea reprezentata este negativa si tot ce ne ramane este sa gasim modulul acelei valori. Vom realiza acest lucru copiind cuvantul original de la dreapta la stanga pana la copierea unui bit de 1, apoi vom completa bitii ramasi, ii vom copia si in final vom decodifica cuvantul obtinut ca si cum ar fi o reprezentare binara normala.
De exemplu, pentru a decodifica cuvantul 1010, vom observa mai intai ca bitul de semn este1 si deci valoarea pe care o reprezinta este negativa. In consecinta, vom converti cuvantul in 0110, vom observa ca aceasta corespunde valorii 6 si vom trage concluzia ca sablonul original reprezinta valoarea -6.
1.5.3 Adunarea numerelor reprezentate in complement fata de doi
Pentru a aduna valori reprezentate in complement fata de doi, aplicam acelasi algoritm ca si pentru adunarea in binar, cu exceptia faptului ca toate cuvintele binare, inclusiv rezultatul, au aceiasi lungime. Aceasta inseamna ca atunci cand se efectueaza o adunare intr-un complement fata de doi, orice bit suplimentar generat la stanga raspunsului de catre un transport final va fi eliminat. Astfel, "adunand" 0101 si 0010 se obtine 0111, in timp ce "adunand" 0111 si 1011 se obtine rezultatul 0010 (0111+1011 = 10010, care este trunchiat la 0010). Acceptand aceasta conventie, sa consideram cele trei probleme de adunare prezentate in figura 1.24. In fiecare caz in parte, vom codifica valorile utilizand notatia in complement fata de doi (pe patru bitii), vom efectua adunarea asa cum s-a descris anterior si vom decodifica apoi rezultatul inapoi in notatia zecimala.
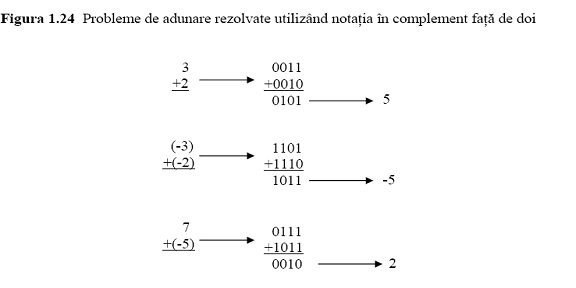
Observati ca daca ar fi sa folosim tehnicile uzuale invatate in scoala primara, a treia problema ar fi un proces complet diferit de problemele precedente (este vorba de operatia de scadere).
Pe de alta parte, prin trecerea problemelor in notatia in complement fata de doi, putem calcula raspunsul corect aplicand in toate cazurile aceleasi algoritm de adunare. Aceasta este prin urmare avantajul notatiei in complement fata de doi: adunarea oricarei combinatii de numere cu semn se poate efectua utilizandu-se acelasi algoritm.
De exemplu, operatia de scadere 7- 5 este identica cu problema de adunare 7 + (-5). In consecinta, daca i se cere unui calculator sa scada 5 (stocat sub forma 0101) din 7 (stocat ca 0111), acesta va schimba mai intai pe 5 in -5 (reprezentat ca 1011) si apoi va efectua adunarea 0111 + 1011, obtinand rezultatul 0010, care reprezinta valoarea 2, dupa cum este descris in continuare:
7 01110111
+(-5) -0101 +1011
______
0010
Observam astfel ca atunci ca pentru reprezentarea valorilor numerice se utilizeaza notatia in complement fata de doi, este suficient sa folosim un circuit pentru adunare combinat cu un circuit pentru negarea unei valori pentru a rezolva atat problema adunarii, cat si pe cea a scaderii numerelor. Dar avantajele nu se opresc aici. Inmultirea este de fapt adunarea repetata, iar impartirea reprezinta scaderea repetata (6/2 reprezinta de cate ori poate fi scazut 2 din 6 fara sa se obtina un rezultat negativ). Astfel ca, in ultima instanta, putem efectua toate cele patru operatii aritmetice standard, adica adunarea, scaderea, inmultirea si impartirea, utilizand doar cele doua circuite.
1.5.4 Problema depasirii superioare
O problema pe care am evitat-o in problemele precedente este aceea ca in oricare dintre sistemele de numeratie pe care le-am prezentat exista o limita privind marimea pe care pot so reprezinte valorile. Atunci cand utilizam notatia in complement fata de doi cu cuvinte de patru biti, valoarea 9 nu are asociata nici un sablon, asa ca nu este nici o sansa sa obtinem un raspuns corect la efectuarea adunarii 5 + 4. De fapt, rezultatul va fi -7. O problema similara apare daca utilizam cuvinte cu lungimea de cinci biti si incercam sa reprezentam valoarea 17.
O astfel de problema poata numele de depasire superioara (overflow). Atunci cand utilizam notatia in complement fata de doi, eroarea de depasire superioara poate aparea la adunarea a doua valori pozitive sau la adunarea a doua valori negative. In fiecare dintre cazuri, depasirea poate fi detectata prin verificarea bitului de semn a raspunsului. Aceasta inseamna ca este semnalata depasirea superioara daca adunarea a doua valori pozitive produce ca rezultat un sablon ce corespunde unei valori negative sau daca rezultatul adunarii a doua valori negative apare ca fiind pozitiv.
Multe calculatoare utilizeaza cuvinte de 32 de biti pentru stocarea valorilor utilizand notatia in complement fata de doi, permitand astfel lucrul cu valori de pana la 2.147.483.647, fara aparitia depasiri superioare. Daca sunt necesare si valori si mai mari, se foloseste adesea tehnica denumita dubla precizie (double precision); ea permite ca lungimea cuvintelor utilizate sa fie marita fata de cea utilizata de obicei de catre calculator.
7. Stocarea numerelor fractionare. Notatia in virgula mobila. Erori de rotunjire (1.6: 1.6.1, 1.6.2)
Sa explicam notatia in virgula mobila printr-un exemplu care utilizeaza numai un octet pentru efectuarea stocarii. Cu toate ca de obicei calculatoarele lucreaza cu cuvinte mult mai lungi, acest exemplu este reprezentativ pentru sistemele actuale si serveste pentru a prezenta concepte importante, fara sa ne complicam folosind cuvinte lungi. Vom considera cel mai semnificativ bit din cadrul octetului ca fiind bitul de semn. Din nou, bitul de semn egal cu 0 inseamna ca valoarea stocata este pozitiva, iar 1 inseamna ca valoarea este strict negativa.
Impartim apoi cei sapte biti ramasi in doua grupuri de campuri, campul exponentului(exponent field) si campul mantisei (mantissa field). Sa consideram cei trei biti care urmeaza dupa bitul de semn ca fiind campul exponentului, iar cei patru biti ramasi ca fiind campul mantisei.
Putem explica semnificatia acestor campuri considerand urmatorul exemplu. Sa presupunem ca un octet contine sirul de biti 01101011. Analizand acest cuvant conform formatului precedent, putem vedea ca bitul de semn este 0, exponentul este 110, iar mantisa este 1011.
Pentru a decodifica octetul, extragem mai intai mantisa si plasam o virgula (punct) zecimala la stanga ei, obtinand .1011
Apoi, extragem continutul campului exponentului (110) si-l interpretam ca pe un intreg stocat utilizand metoda in exces pe trei biti. In acest caz, cuvantul binar din campul exponentului reprezinta valoarea pozitiva 2. Acest fapt ne precizeaza ca trebuie sa mutam virgula la dreapta cu doi biti. (Un exponent negativ inseamna ca virgula trebuie deplasata la stanga.) In consecinta, obtinem 10.11 care inseamna 2 3/4. Observam apoi ca bitul de semn din exemplul considerat este 0; valoarea reprezentata este pozitiva. Vom trage concluzia ca 01101011 reprezinta valoarea 2 3/4. Inainte de a trece mai departe, sa explicam de ce este utilizata notatia in exces pentru reprezentarea exponentului in cazul sistemelor in virgula mobila. Utilizarea notatiei in exces reduce operatia de comparare a marimii relative a doua valori la simpla parcurgere a reprezentarilor de la stanga la dreapta, pana la intalnirea primului bit care difera. De exemplu, daca ambii biti de semn sunt zero, cea mai mare dintre cele doua valori este aceea care are 1 pe pozitia primului bit care difera la parcurgerea de la stanga la dreapta celor doua cuvinte.
Astfel, daca 00101010 si 00011001 sunt reprezentari in virgula mobila, vom putea afirma ca prima reprezentare corespunde unei valori mai mari, fara a trebui sa determinam mai intai valorile care corespund efectiv celor doua reprezentari.
1.6.2 Erori de rotunjire
Pe scurt, atunci cand sunt adunate valori reprezentate in notatia in virgula mobila, ordinea in care se fac operatiile poate fi extrem de importanta. Regula generala este ca intotdeauna sa fie adunate mai intai valorile cele mai mici; totusi, nici macar acest mod de lucru nu garanteaza corectitudinea rezultatului.
12. Executia programelor (2.3)
2.3 Executia programelor
Calculatorul urmareste un program stocat in memorie copiind instructiunile din memorie in unitatea de comanda pe masura ce are nevoie de ele. O data ajunsa in unitatea de comanda, fiecare instructiune este decodificata si executata. Ordinea in care sunt extrase instructiunile din memorie corespunde ordinii in care acestea sunt stocate, cu exceptia cazului in care o instructiune JUMP specifica altceva. Pentru a intelege cum se desfasoara procesul de executiea unui program trebuie sa studiem mai amanuntit unitatea de comanda din interiorul CPU. Ea contine doi registri cu destinatie speciala: contorul programului (program counter) si registrul de instructiuni (instruction register), asa cum se poate observa in figura 2.4.
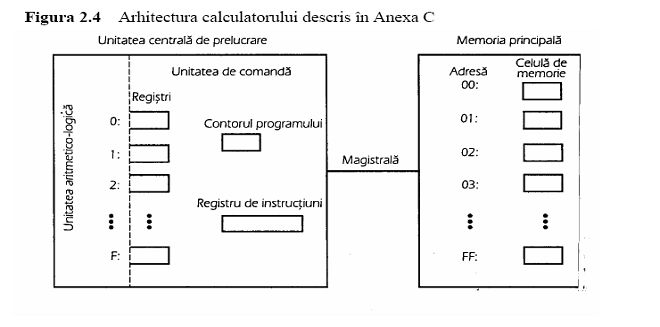
Registrul contorului programului contine adresa urmatoarei instructiuni care trebuie executata, permitand astfel calculatorului sa urmareasca locul in care se afla in program. Registrul de instructiuni este utilizat pentru stocarea instructiunii in curs de executie.
Unitatea de comanda isi realizeaza sarcinile repetand continuu un algoritm, denumit ciclul masinii (machine cycle), care consta din trei pasi: extragere (fetch), decodificare si executie (figura 2.6). In timpul pasului de extragere, unitatea de comanda solicita memoriei principale sa-i furnizeze urmatoarea instructiune care va fi executata. Unitatea stie unde se afla urmatoarea instructiune in memorie deoarece adresa acesteia se afla in registrul contorului programului. Unitatea de comanda plaseaza instructiunea receptionata din memorie in registrul sau de instructiuni si incrementeaza apoi contorul programului astfel incat acesta sa contina adresa urmatoarei instructiuni.
Avand acum instructiunea in registrul de instructiuni, unitatea de comanda incepe faza de decodificare din ciclul masinii. In acest punct, ea analizeaza campurile codului de operatie si operanzilor pentru a determina ce actiuni trebuie efectuate.
Dupa decodificarea instructiunii, unitatea de comanda intra in faza de executie, in timpul careia activeaza circuitele adecvate pentru realizarea actiunilor solicitate. De exemplu, daca instructiunea se refera la incarcarea datelor din memorie, unitatea de comanda face sa se efectueze operatia de incarcare; daca instructiunea se refera la o operatie aritmetico-logica, unitatea de comanda activeaza circuitele adecvate din unitatea aritmetico-logica, avand ca intrari registrii corespunzatori.
Dupa executia instructiunii unitatea de comanda incepe un nou ciclu al masinii cu faza de extragere. Observati ca deoarece contorul programului a fost incrementat la sfarsitul fazei precedente de extragere, el furnizeaza din nou unitatii de comana adresa corecta a instructiunii.
Un caz ceva mai aparte este reprezentat de executia unei instructiuni JUMP. Consideram de exemplu instructiunea B258, care se traduce ca "JUMP la instructiunea de la adresa 58 daca continutul registrului 2 este identic cu cel al registrului 0". in acest caz, faza de executie din ciclul masina incepe cu compararea registrilor 2 si 0. Daca cei doi registri difera, faza de executie se termina si incepe urmatoarea faza de extragere. Daca insa continutul celor doi registri este identic, unitatea de comanda plaseaza valoarea 58 in contorul programului inainte de a termina faza de executie. In aceasta situatie, urmatoarea faza de extragere incepe cu valoarea 58 in contorul programului, asa ca instructiunea de la acea adresa va deveni prima instructiune de executat.