|
|
|
Dupa cum se cunoaste orice suprafata de teren este definita atat de limitele acesteia cat si de detaliile sale naturale (dealuri, vai, paduri, ape etc.) si artificiale (cai de comunicatie, poduri, canale, localitati etc.). De asemenea orice detaliu topografic (contur, inaltime, linie etc.) poate fi determinat de punctele sale caracteristice, puncte judicios alese si suficient de dese, conform preciziei cerute pentru ridicare.
Se considera puncte topografice caracteristice toate punctele de schimbare a directiei pentru liniile detaliului, precum si cele de schimbare a pantei, iar alegerea pe teren s unui numar minim de astfel de puncte reprezinta geometrizarea figurilor neregulate din teren, atat in plan cat si in inaltime (Fig. 4).
Fig. 4. Geometrizarea sinuozitatilor de pe teren
a) in plan; b) in inaltime
Determinarea punctelor topografice se realizeaza prin coordonate rectangulare plane (X si Y) si prin cote absolute (Z), stabilite fata de un sistem de referinta.
Daca punctele A si B (Fig. 5) sunt marcate pe teren prin tarusi sau borne pe teren, vom deosebi urmatoarele elemente topografice:
Aliniamentul AB - este directia materializata pe teren, ce rezulta din intersectia suprafetei terenului cu un plan vertical ce trece prin cele doua puncte; in plan aliniamentul reprezinta o linie dreapta obtinuta ca rezultat al geometrizarii suprafetei terenului.
Fig. 5. Elementele topografice ale terenului
Distanta inclinata AB = L - este segmentul de linie inclinata ce uneste punctele A si B din spatiu.
Distanta orizontala AB'=D - este proiectia distantei inclinate AB pe un plan orizontal, iar valoarea acesteia se poate obtine si indirect.
D = L cos
Altitudinea punctului A(
) este
distanta verticala masurata de la punctul topografic
respectiv pana la suprafata de nivel zero, care este suprafata
de nivel mediu a apelor linistite ale marilor si oceanelor,
presupusa, prelungita pe sub continente, numita Geoid.
Diferenta de nivel ( Z AB) - este distanta masurata pe verticala intre punctul B si planul orizontal ce trece prin punctul A.
Unghiul de panta al terenului - este unghiul vertical (vezi Fig. 14) situat in planul vertical ce trece prin punctele A si B si pe care il face dreapta inclinata AB = L, cu planul orizontal.
Atunci cand planul de referinta este vertical, va rezulta complementul unghiului vertical , adica unghiul zenital Z. De asemenea, cand nu se cunosc cotele ambelor puncte topografice A(ZA) si B (ZB), diferenta de nivel (Z) se va obtine cu ajutorul distantei si unghiului vertical, astfel:
ZAB = + L sin = + D ctg
sau
ZAB = + L cos Z = + D ctg z
Unghiul
orizontal (Fig. 6) - este
unghiul intre proiectiile orizontale a doua linii de vizare cu
teodolitul, masurate pe cercul orizontal al acestuia, iar valoarea
acestuia se obtine din diferenta valorilor a doua directii
(
si 
), cu relatia:
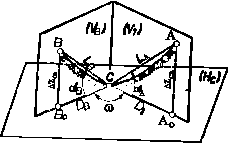
Fig. 6. Unghiul orizontal determinat din diferenta a doua directii
Orientarea unei directii
, este
unghiul care se formeaza intre o directie de referinta
avand o pozitie cunoscuta (ex. C-
) si o
alta directie oarecare masurata intotdeauna in sensul
acelor de ceasornic. Putem utiliza nordul geografic Ng sau nordul magnetic Nm,
obtinand in acest sens fie orientari geografice g, fie
orientari magnetice 
(Fig. 7).
Pentru planurile topografice executate la scara mare, necesare proiectarii constructiilor curente, distanta maxima intre doua puncte este de 4 km, ceea ce permite sa se aproximeze ca directiile nordului geografic in cele doua puncte sunt paralele, adica unghiul de convergenta meridiana 0, iar sistemul rectangular de referinta pentru raportarea punctelor pe plan se alege astfel ca axa OX sa fie paralela cu directia nordului.
Fig. 7. Determinarea coordonatelor punctelor in plan
In vederea definirii pozitiei directiei AB, se va duce directia nordului prin punctul A, constatandu-se mai multe directii astfel:
a.
directia
ANm - este directia nordului magnetic fata de care
dreapta AB formeaza unghiul - azimutal ce se masoara cu busola;
b. directia ANg - este directia nordului geografic al punctului A; unghiul de orientare pe care il face dreapta AB cu directia meridianului geografic al punctului A, numit si azimutul geografic al directiei AB, notata cu Az;
c. directia A Ng O paralela in A la directia meridianului geografic al originii O a sistemului de axe rectangulare fata de care este definita dreapta AB; unghiul reprezinta orientarea dreptei fata de paralela din A la meridianul axial OX.
Trecerea la orientarea geografica se face conform figurii 7, cu relatiile
unde: - unghi de convergenta meridiana, fiind unghiul pe care il fac tangentele la meridianele geografice a doua puncte, in cazul dat O si A. Daca distanta dintre cele doua puncte este mai mica de 40.50 km, valoarea convergentei se va calcula cu relatia simplificata:
= sin
unde: - este diferenta de longitudine
- latitudinea medie a
celor doua puncte
- unghi de
inclinatie magnetica format intre meridianul geografic si cel
magnetic
Pozitia in plan a punctelor topografice este data de coordonatele lor rectangulare (X, Y), iar pozitia unui punct B in functie de pozitia cunoscuta a punctului A este:
XB = XA + XAB
YB = YA + YAB
in care: X si Y sunt coordonatele relative, sau cresterile de coordonate care se exprima trigonometric in functie de distanta redusa la orizont dintre cele doua puncte A si B si de orientarea laturii AB dupa directia NgO;
X = D cos AB
Y = D sin AB
In orice sistem de referinta
orientarile se calculeaza intotdeauna dupa o paralela la
directia nordului a originii sistemului dusa prin punctul respectiv,
iar orientarile inverse difera cu 
plus convergenta meridianelor, astfel:
