Regimul nesimetric

_{Regimul nesimetric}

1. Bazele analitice ale regimului nesimetric

Un sistem polifazat de tensiuni sau curenti poate avea caracteristici diferite pe faze, in ceea ce priveste valorile efective sau fazele marimilor periodice, sinusoidale, componente ale sistemelor respective. In consecinta, pentru un sistem nesimetric de marimi alternative, sinusoidale (Y₁, Y₂, Y₃) se poate determina setul de componente simetrice, format din marimile de succesiune (secventa) directa (pozitiva) Y_d, inversa (negativa) Y_i si omopolara (de succesiune zero) Y_h, in baza teoremei Stokvis-Fortesque:

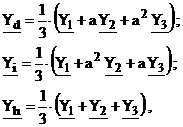(2.109)

in care este operatorul de rotatie, iar sistemul trifazat de fazori (Y₁, Y₂, Y₃) poate fi relativ la tensiuni sau curenti. Referitor la terminologie, se prefera utilizarea ambelor familii de notiuni, atat a celei consacrate, denumind componentele simetrice de succesiune directa, inversa si omopolara, cat si a celei propagate sub influenta literaturii de specialitate, anglo-saxone, denumind aceleasi componente respectiv de succesiune pozitiva, negativa si zero; termenul omopolar este preferat in locul celui de "homopolar", desi pentru marimile de aceasta succesiune se foloseste indicele h. De asemenea, pentru marimile de succesiune directa (pozitiva) si inversa (negativa) s-a optat pentru notarea cu indicii d, respectiv i, in loc de a se folosi notatiile propuse cu semne de polaritate (+, respectiv -), la exponent, notatii care vor fi insa prezentate ca alternativa, din motive de usurare a identificarii. Optiunile de mai sus sunt justificate, pe de o parte, de existenta unui numar mare de specialisti familiarizati cu denumirile consacrate, iar pe de alta parte de confuziile care pot fi create prin utilizarea de semne de polaritate la exponent si de evitarea exprimarilor de forma "componenta de secventa zero este zero" sau "cazul componentei de secventa zero nule".

Determinarea fazoriala a sistemelor de tensiuni si curenti necesita aparatura de masura mai complexa si stocarea simultana a datelor, ceea ce face ca aparatele de masura clasice sa fie excluse din discutie. Se pot folosi echipamente de caracterizare a CEE de tip calimetru (Powermeter) sau sisteme de achizitie de date, conectate la calculator.

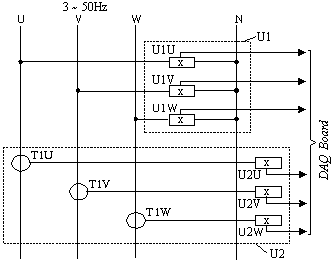
Fig. 2.24. Conectarea traductoarelor cu efect Hall, de tensiune si curent, pentru achizitia

tensiunilor de faza, respectiv a curentilor de linie: T1-transformatoare de masura, de curent;

U1-traductoare de tensiune; U2-traductoare de curent; DAQ Board - placa de achizitie.

In figura 2.24, se prezinta schema electrica de conectare a traductoarelor de tensiune si curent, cu efect Hall, pentru achizitionarea sistemelor de tensiuni de faza si de curenti de linie. De remarcat faptul ca sistemul de conductoare contine si conductorul neutru, deci sistemul este cu neutru accesibil, iar nivelurile tensiunilor permit conectarea directa a traductoarelor de tensiune; traductoarele U1U, U1V si U1W furnizeaza semnale proportionale cu tensiunile de faza. In acest caz, sistemul tensiunilor de linie nu trebuie sa fie achizitionat, deoarece acesta poate fi reconstituit pe baza sistemului de tensiuni de faza. La conceperea schemei, s-a admis faptul ca traductoarele de curent, U2U,U2V si U2W, nu pot fi conectate direct in circuit, datorita valorilor importante ale curentilor, asfel ca utilizarea transformatoarelor de masura T1U, T1V si T1W este necesara; aceste transformatoare trebuie sa fie de precizie si sa furnizeze un semnal nedistorsionat traductoarelor de curent corespunzatoare. Semnalele de la iesirile traductoarelor de tensiune si de curent sunt trimise spre placa de achizitii de date, DAQ Board [14].

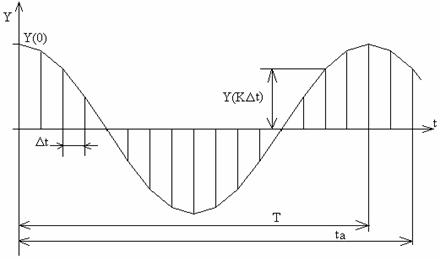
Fig. 2.25. Marime periodica, esantionata, pentru achizitia de date.

Daca nivelul tensiunilor de faza depaseste 1 kV, sunt necesare transformatoare de masura, de tensiune la achizitionarea tensiunilor de faza, acestea trebuind sa indeplineasca aceleasi conditii, expuse in legatura cu transformatoarele de masura, de curent.

Din sirul de valori Y(k Dt), pe care placa de achizitie il furnizeaza calculatorului pentru o anumita marime Y, trebuie mai intai sa se determine perioada reala, din care apoi rezulta frecventa reala, iar in continuare se identifica amplitudinea si faza fundamentalei, pentru fiecare marime achizitionata, folosind o analiza Fourier discreta, restransa la acest obiectiv. In figura 2.25, se prezinta marimile caracteristice achizitiei de date pe un canal si marimea periodica, sinusoidala, corespunzatoare.

Daca si sunt cele doua sisteme de marimi achizitionate, al tensiunilor de faza, respectiv al curentilor de linie, sistemul tensiunilor de linie poate fi determinat prin calcul. In figura 2.26, se prezinta 'steaua' tensiunilor de faza, triunghiul tensiunilor de linie si sistemul de fazori al curentilor de linie.

Unghiurile dintre fazorii tensiunilor de faza, precizate prin literele de la indici, se determina cu relatiile:

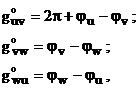(2.110)

in care sunt fazele tensiunilor de faza. Sistemul tensiunilor de linie poate fi acum complet determinat. Modulele fazorilor reprezentand tensiunile de linie se calculeaza cu relatiile:

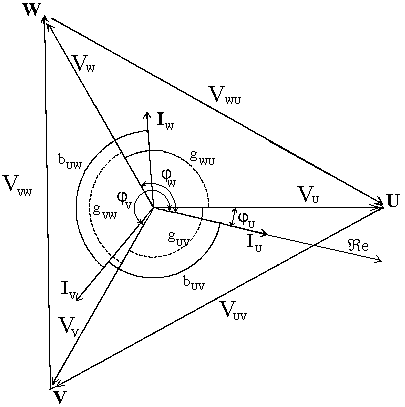
Fig. 2.26. Sistemele tensiunilor de faza si de linie si a curentilor de linie, in reprezentare fazoriala.

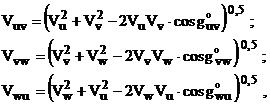(2.111)

reprezentand amplitudini sau valori efective, dupa semnificatiile respective ale tensiunilor de faza . Fazele din planul complex al tensiunilor de linie rezulta sub forma:

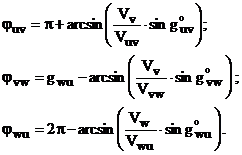(2.112)

Cele trei sisteme de marimi trifazate fiind fazorial complet determinate, se poate trece la analiza regimului nesimetric.

2. Calculul componentelor simetrice

Este evident faptul ca aprecierea regimului nesimetric se poate face numai in baza componentelor simetrice, determinate pe baza teoremei Stokvis-Fortesque. Sublinierea este importanta in contextul proliferarii de relatii de calcul, care improvizeaza caracterizarea regimului nesimetric, inclusiv in ceea ce priveste relatiile implementate in echipamente de tip calimetru sau Powermeter.

In consecinta, componentele simetrice se calculeaza riguros pe baza relatiilor (2.109), care prezinta insa dezavantajul ca sunt in complex, existand mai putine medii de programare, destinate a lucra in acest plan.

a) Metoda de calcul iterativ

S-a procedat la dezvoltarea relatiilor (2.109) prin explicitarea operatorilor a si a² si separarea partilor reale si imaginare, in vederea determinarii, in principal, a modulelor componentelor simetrice, acestea fiind necesare la caracterizarea regimului nesimetric [14]. Astfel, pentru componenta de succesiune directa (pozitiva) Y_d se obtine mai intai, in complex, relatia:

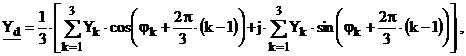(2.113)

din care se deduce modulul Y_d al acesteia sub forma

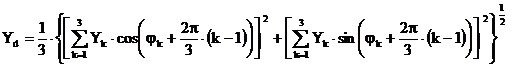, (2.114)

care se preteaza unui calculul iterativ.     Similar, printr-un artificiu de calcul, s-a dedus relatia potrivita calculului iterativ pentru componenta de succesiune inversa (negativa)

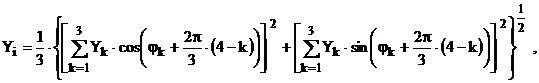(2.115)

precum si pentru componenta omopolara (de secventa zero)

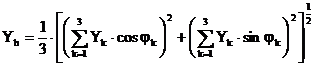, (2.116)

astfel incat setul de relatii (2.114)÷(2.116) constituie o baza de calcul scalar, iterativ a componentelor simetrice. De remarcat faptul ca, pe baza relatiilor de forma (2.113), se pot determina si fazele componentelor simetrice, partile reala si imaginara ale expresiilor aparand in aceasta ordine.

b) Metoda geometrica

Asa cum s-a semnalat deja, exista si alte metode de calcul a componentelor simetrice sau, direct, a unor indicatori ai regimului nesimetric [10,12]. Prima care se impune a fi semnalata este metoda care poate fi denumita geometrica, deoarece se bazeaza pe rezolvarea triunghiurilor (lui Napoleon) care evidentiaza constructia componentelor simetrice. Intr-o prima forma, valabila pentru cazul in care componenta omopolara (de succesiune zero) este nenula

metoda geometrica ofera urmatoarele relatii de calcul a componentelor de succesiune directa (pozitiva) si inversa (negativa):

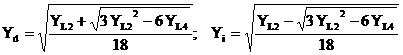(2.117)

in care s-au considerat urmatoarele notatii

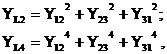(2.118)

iar (Y₁₂, Y₂₃, Y₃₁) reprezinta sistemul marimilor de linie, dat de relatiile in complex

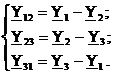(2.119)

Se observa faptul ca, desi se calculeaza componentele simetrice pentru sistemul marimilor de faza, sunt necesare si marimile de linie.

In cazul componentei omopolare nule, relatiile de calcul propuse sunt urmatoarele:

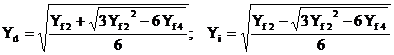(2.120)

in care notatiile introduse au semnificatiile de mai jos:

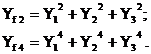(2.121)

c) Relatia Robert-Marquet

Rezultate identice cu metoda geometrica furnizeaza relatia Robert - Marquet, data direct pentru calculul raportului dintre componenta inversa si cea directa (aplicabila daca Y_h=0):

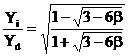(2.122)

in care s-a introdus notatia

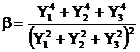. (2.123)

d) Metoda GOST

Denumirea metodei deriva din termenul (GOST) prin care se desemneaza standardele rusesti, deoarece este propusa intr-un asemenea document. Mai intai, se indica urmatoarea relatie de calcul a componentei inverse (de succesiune negativa), aplicabila pentru cazul componentei omopolare nule (Y_h=0, de ex. in cazul sistemului de tensiuni de linie):

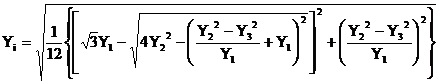. (2.124)

Calculul componentei omopolare (de succesiune zero) este indicat numai pentru sistemul tensiunilor de faza, deoarece trebuie cunoscute si tensiunile de linie. Relatia de calcul a componentei omopolare este

, (2.125)

in care se considera urmatoarele notatii:

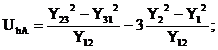(2.126)

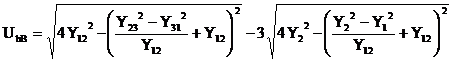, (2.127)

iar sistemul tensiunilor de linie se determina cu relatiile (2.119).

Metoda nu indica modalitatea de calcul a componentei directe (de succesiune pozitiva), ceea ce inseamna ca, pentru aceasta componenta, ar trebui folosita prima relatie din sistemul (2.109).

e) Relatii simplificate

Deoarece relatiile de calcul al componentelor simetrice, fie acestea (2.109) sau (2.113)÷(2.127), sunt destul de complicate, s-a propus in literatura de specialitate o serie de relatii simplificate, care sa caracterizeze totusi regimul nesimetric, dar cu o anumita eroare, limitata.

Metoda denumita aici GOST, cu eroare indica mai intai relatia de calcul a componentei de succesiune inversa (negativa), pentru cazul componentei omopolare nule (Y_h=0):

Y_i = 0,62 (Y_Max - Y_min), (2.128)

precum si a componentei omopolare a sistemului de tensiuni de faza

U_h = 0,62 (U_fMax - U_fmin) , (2.129)

apreciindu-se la 8 % eroarea de aproximare prin aceste relatii simplificate.

O alta metoda simplificata, care ar putea fi denumita a abaterii maxime, raportata la valoarea medie, raporteaza diferenta dintre cea mai mare si cea mai mica valoare, la valoarea medie aritmetica a celor trei marimi, conform relatiei

, (2.130)

pentru a determina un factor k_nes, apreciat ca relevant pentru gradul de nesimetrie. Deoarece consideratiile implicate in aceasta metoda nu au la baza nimic din aspectul profund fazorial al regimului nesimetric, valorile calculate cu relatia (2.130) nu coreleaza deloc cu vreo marime adimensionala, determinata din marimile calculate cu teorema Stokvis-Fortesque, asa cum se va putea constata in cadrul paragrafului 5.

3. Indicatori ai regimului nesimetric

Caracterizarea nesimetriei unui sistem polifazat se realizeaza prin indicatori calculati ca rapoarte dintre componentele de succesiune inversa (negativa) sau omopolara (zero), pe de o parte, si componenta de succesiune directa (pozitiva) sau valoarea nominala corespunzatoare, pe de alta parte. Coeficientii sau factorii definiti in cele ce urmeaza se noteaza cu litera K si, fiind marimi obtinute prin raportare, li se atribuie ca prim indice pe cel al marimii de la numarator, iar ca al doilea indice, pe cel al marimii de la numitor, notatia avand astfel o anumita expresivitate.

a) Coeficientul de disimetrie, denumit si factor de nesimetrie negativa (notatie propusa in [22] - ), este definit prin raportul procentual dintre componenta de succesiune inversa (negativa) Y_i si cea de succesiune directa (pozitiva) Y_d, dat de relatia

(2.131)

b) Coeficientul de asimetrie, denumit si factor de nesimetrie zero (notatie propusa in [22] - ), se defineste prin raportul dintre componenta omopolara (de succesiune zero) si cea de succesiune directa (pozitiva), raport exprimat in procente:

. (2.132)

c) Coeficientul de succesiune inversa se determina prin raportarea valorii efective a componentei de succesiune inversa (negativa) la valoarea nominala, care, pentru tensiuni, conduce la expresia in procente

(2.133)

in care U_i reprezinta valoarea efectiva a tensiunii de succesiune inversa, pentru frecventa fundamentala a sistemului trifazat de tensiuni, iar U_n - tensiunea nominala, corespunzatoare sistemului de tensiuni, pentru care s-a determinat U_i.

d) Coeficientul de succesiune omopolara se obtine prin raportarea valorii efective a componentei omopolare (de succesiune zero) la valoarea nominala, conform relatiei scrisa direct pentru tensiunile de faza

(2.134)

avand in vedere faptul ca sistemul tensiunilor de linie nu are componenta omopolara

5. Valori limita ale indicatorilor de regim nesimetric

Normele privind regimurile nesimetrice se refera la componenta de secventa negativa a sistemului de tensiuni, prin indicarea valorilor limita ale factorilor de nesimetrie negativa si mai rar ale factorilor de nesimetrie zero, precum si a factorilor de nesimetrie pentru curenti.

Conform normelor stabilite de CEI, se recomanda urmatoarele valori limita ale coeficientilor de disimetrie (succesiune negativa), in functie de clasele de mediu electromagnetic:

K_idMax = 2% pentru instalatii din clasele 1 si 2;

K_idMax = 3% pentru instalatii din clasa a 3-a.

In Romania, valorile limita, maxime, ale coeficientilor de succesiune negativa (disimetrie), pentru sistemele de tensiuni, sunt dupa cum urmeaza [22]:

2% - pentru retelele de JT si MT, precum si in nodul de racord al unei substatii de tractiune electrica;

1% - pentru retele de IT.

Conform standardelor romanesti, sistemul tensiunilor de alimentare a transformatoarelor electrice este considerat practic simetric, daca coeficientul de asimetrie maxim este K_{hd Max}=2%, iar in cazul masinilor electrice rotative K_{hd Max}=1%.