Utilizarea SPSS in analiza designurilor factoriale

Utilizarea SPSS in analiza designurilor factoriale

Obiective operationale:

Dupa lectura acestui capitol, studentii ar trebui sa reuseasca sa:

elaboreze baza de date corespunzatoare unui studiu unifactorial si bifactorial

calculeze indicatorii statistici ai principalelor efecte vizate in designurile factoriale

sa efectueze comparatiile post-hoc

interpreteze rezultatele obtinute

A. Calculul statistic inferential al datelor rezultate dintr-un design unifactorial cu esantioane independente

O practica impusa in cercetarea efectului medicamentelor este de a implica in studiu un grup de placebo. Conform acestui plan, autorii unui studiu ipotetic isi propun sa verifice eficienta unui nou medicament in tratamentul depresiei. In acest scop selecteaza 30 de voluntari cu diagnostic clinic depresie, si ii randomizeaza in trei grupe: control, placebo si experimental. Pacientii grupului experimental primesc medicatie antidepresiva; pacientii din grupul placebo primesc un medicament care nu contine substanta activa; si pacientii grupul de control nu primesc nici o medicatie. Variabila dependenta o reprezinta intensitatea simptomatologiei inregistrata pe o scala de la 1-20 (1=depresie redusa si 20=depresie accentuata).  Rezultatele obtinute sunt prezentate in tabelul de mai jos.

In baza de date vom defini doua variabile, una pentru variabila independenta (denumita grup) cu trei valori (1=grup control, 2=grup placebo si 3=grup experimental) si o variabila (denumita scor) pentru a inregistra scorurile masurate. Pentru a verifica semnificativitatea statistica a diferentelor vom recurge la analiza de varianta pentru design unifactorial cu esantioane independente. Pentru a calcula valoarea testului F vom urma calea Analyze→Compare means→One-Way Anova. In rubrica Dependent list vom introduce variabila masurata (denumita scor) si in ribrica Factor vom introduce variabila care defineste grupele variabile independente. La sectiunea Options vom bifa Descriptives pentru a obtine datele descriptive si Homogeneity of variance test pentru a verifica asumptia omogenitatii variantelor in populatie. La optiunea Post-Hoc vom bifa una din optiunile de comparatie post-hoc, de obicei se utilizeaza Tukey sau Scheffe, in acest caz vom apela la cel de-al doilea. Rezultatele ferestrei output sunt cele prezentate mai jos.

Descriptives

In acest tabel avem datele descriptive ale celor trei esantioane (N, Mean, Std. Deviation si Std. Error), precum si intervalele de incredere (Lower Bound si Upper Bound) si intervalul de variabilitate a datelor (Minimum si Maximum). Se observa ca exista diferente intre mediile celor trei esantioane, cel mai amre scor il are grupul de control si cel mai mic apartine grupului experimental. Rezultatul oferit de testul de omogenitate al variantelor este nesemnificativ, p=0.8 (mai mare decat 0.05), ceea ce inseamna ca datele satisfac criteriul omogenitatii variantei in populatie. Pentru a verifica daca cel putin una din diferentele posibile (intre grupele 1-2, 1-3, 2-3) este semnificativa vom citi tabelul umator.

ANOVA

Raportul dintre varianta inter- si varianta intra-grup rezulta un F(2,27)=7,158. Probabilitatea acestei valori pe baza ipotezei nule, adica probabilitatea de a obtine o asemenea valoare prin selectia aleatoare a trei esantioane dintr-o populatie este p=0.003, mult mai mica decat valoarea prag (0.05). In baza acestui rezultata putem afirma cel putin una din comparatiile posibile este semnificativa statistic. Pentru a verifica, care dintre aceste comparatii este aceea vom citi tabelul comparatiilor post-hoc.

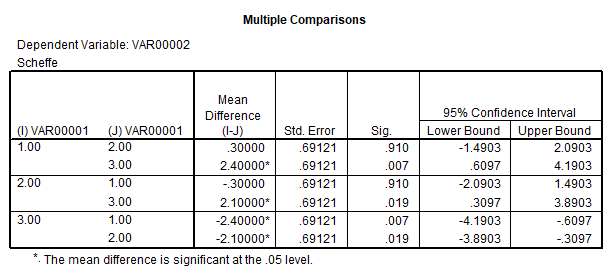
Tabelul oferit de SPSS este unul redundant, din moment ce ne ofera toate comparatiile posibile (ex. Intre grupele 1 si 2, respectiv intre grupele 2 si 1). In tabel vom urmari Mean Difference (diferentele de medii), Std. Error (eroarea standard), Sig. (valoarea calculata a lui p) si Confidence interval (intervalul de incredere). Se observa ca numai diferenta dintre grupele 1-3 si 2-3 este semnificativa, valoarea calculata a lui p pentru prima comparatie este 0,007 si 0.019 pentru a doua, ambele fiind mai mici decat valoarea prag (0,05). Acest fapt este confirmat si de intervalul de incredere afisat, numai in cazul acestor comparatii intervalul nu include valoarea 0, restul diferentelor fiind nesemnificativa.

Datele obtinute sustin eficienta unui efect al interventiei medicamentoase, rezultatele obtinute de acest difera semnificativ atat de grupul de control cat si de grupul placebo. Nu s-a constatat nici o diferenta intre grupul de control si grupul placebo, ceea ce indica o absenta a efectului placebo in acest studiu.

B. Calculul statistic inferential al datelor rezultate dintr-un design bifactorial cu esantioane independente

Pentru a exemplifica modul de prelucrare a datelor obtinute intr-un design bifactorial, vom analiza un alt studiu ipotetic. Un grup de cercetatori a incercat sa investigheze diferentele existente in memoria verbala a subiectilor tineri si varstnici. In acest scop a selectat aleator un grup de subiecti tineri (20) si un grup de subiecti varstnici (20). Dar pentru ca exista diferente de gen in ceea ce priveste abilitatea verbala generala, cercetatorii au hotarat sa includa in studiu si variabila gen (femei si barbati). Variabila masurata a acestui cvasi-experiment este numarul de cuvinte reactualizate in proba de memorie. Rezultatele obtinute sunt prezentate in tabelul de mai jos.

In baza de date vom defini trei variabile, doua pentru variabilele independente ale cercetarii. Prima variabila denumita varsta va avea doua modalitati, 1=tineri si 2=varstnici, a doua variabila gen tot cu doua modalitati 1=femei si 2=barbati. In a treia variabila (denumita scor) vom introduce valorile variabilei masurate. Datele colectate vor fi analizate prin ANOVA bifactorial 2x2. Pentru a efectuat aceasta analiza vom urma sirul de comenzi Analyze→General Linear Model→Univariate . In rubrica Dependent list vom introduce variabila dependenta Scor, si in rubrica Fixed factors vom introduce variabilele independente ale modelului, Varsta si Gen. La Options vom cere afisarea mediilor pentru toate efectele (varsta, gen si varsta*gen). Pentru a derula procesare vom apasa OK. Rezultatele obtinute sunt prezentate mai jos. In primul tabel este reprezentat structura designului utilizat si efectivul fiecarei casute.

Between-Subjects Factors

Pe aceeasi structura, tabelul urmator afiseaza datele statistice descriptive (medie si abatere standard pentru fiecare casuta a designului).

Descriptive Statistics

Tabelul testului de omogenitate a variantelor in populatie si de aceasta data arata ca setul de date respecta asumptia omogenitatii egalitatii variantei in populatie, valoarea calculata a lui p este 0.777, mai mica e decat valoarea prag (0.05). Pentru a verifica semnificativitatea efectelor variabilelor implicate in studiu vom analiza tabelul urmator.

Tests of Between-Subjects Effects

Primele doua linii se refera la abordarea ANOVA din punct de vedere a regresiei (in acest caz vom face abstractie de aceste date). In linia Varsta, Gen si Varsta*Gen observam ca exista un efect al varstei (p calculate este de 0.000 < 0.05), efectul genului nu este semnificativ (p calculat este 0.088 > 0.05) si nu exista efect semnificativ al interactiunii (p calculat este 0.264 > 0.05). Tabele descriptive reiau pentru fiecare variabila informatiile deja prezentate in tabelul general, oferind pentru fiecare si un calcul al intervalului de incredere (vezi exemplul pentru variabila varsta).

1. varsta

Pe baza rezultatelor statistice obtinute putem afirma ca in acest studiu exista un efect principal semnificativ statistic al varstei, insa nu exista diferenta semnificativa de gen si nici efect al interactiunii celor doua variabile.